Apparatus:
Spring and cork, tall retort stand/clamp/boss, set of 100g masses with holder, mirror, long pin, small piece of plasticine, stop watch, plumb line, one metre rule, card with line.
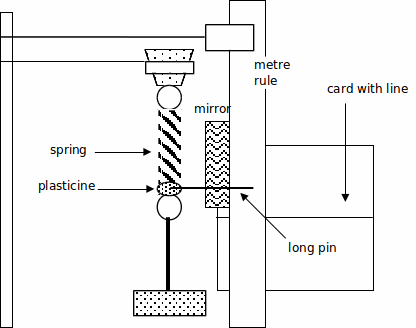
Procedure:
1. Hang the spring vertically from a stand and attach the optical pin pointer onto the end of the spring using a small piece of plasticine. Clamp the metre ruler vertically (check with the plumb line) next to the spring.
2. Note the initial level (
/m) of the optical pin against the ruler, use the mirror to check that your eye is at the same level as the pin.
3. Hang a mass,
(100g plus the mass holder) and then note the new pin level (
/m) and so calculate the spring extension,
where
4. Now displace this mass from its equilibrium position and release. Measure the time for
oscillations
(should be at least 5). Use the line on the card, placed at the mid-point of the oscillations, when counting oscillations. Repeat and so calculate the average time foroscillations.
Finally calculate the period for one oscillation,
/s and also
/ s 2 .
5. Repeat stages 2 to 4 for four other values of
(maximum 700g).
6. Tabulate ALL of your measurements & results.
7. Plot the following graphs: (a) mass,
/ kg against extension,
/ m. (b)/ s 2 against/ kg. Both graphs should be straight lines.
8. The extension,caused by a mass,of weight,
are related by
(1). The period of oscillation of a mass hung from a spring is given by
(2) (where, in both cases,
). When squared the second equation becomes
The gradient of your first graph,
is equal to
It can be shown that the gradient of the second graph,
is given by
hence
Use your graph gradients, and the above relationship, to find a value for the gravitational field strength,
and for the spring constant,
9 (a) How, if at all, would your graphs and results be different if you were to perform this experiment on the moon?
(b) Show how the expression,
is obtained starting from (1) & (2).