\[m_1, \: m_2, \: m_3\]
extended distances \[x_1, \: x_2, \: x_3\]
from their equilibrium positions.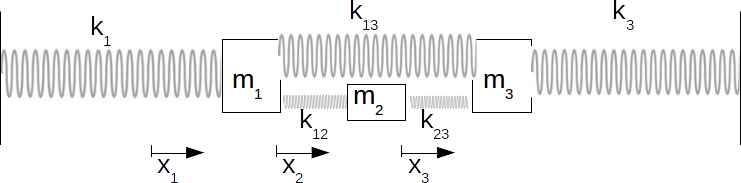
\[m_1\]
: \[-k_1x_1+k_{12}(x_2-x_1)+k_{13}(x_3-x_1)=-(k_1+k_{12}+k_{13})x_1+k_{12}x_2+k_{13}x_3\]
\[m_2\]
: \[-k_{12}(x_2-x_1)+k_{23}(x_3-x_2)=k_{12}x_1-(k_{12}+k_{23})x_2+k_{23}x_3\]
\[m_3\]
: \[-k_{13}(x_3-x_1)-k_{23}(x_3-x_2)-k_3x_3=k_{13}x_1+k_{23}x_2-(k_{13}+k_{23}+k_3)x_3 \]
The stiffness matrix is then
\[K= \left( \begin{array}{ccc} -(k_1+k_{12}+k_{13}) & k_{12} & k_{13} \\ k_{12} & -(k_{12}+k_{23}) & k_{23} \\ k_{13} & k_{23} & -(k_{13}+k_{23}+k_3) \end{array} \right) \]
The elasticity matrix is nbsp;
\[K^{-1}= \left( \begin{array}{ccc} -(k_1+k_{12}+k_{13}) & k_{12} & k_{13} \\ k_{12} & -(k_{12}+k_{23}) & k_{23} \\ k_{13} & k_{23} & -(k_{13}+k_{23}+k_3) \end{array} \right)^{-1} \]
. 