\[\mathbf{F}=m \mathbf{a}\]
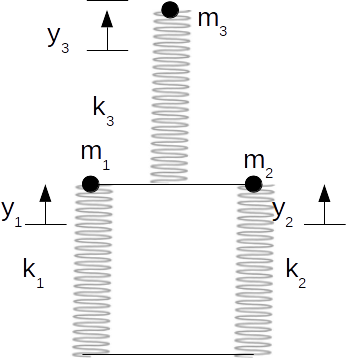
to each particle:\[m_1\]
: \[m_1 \ddot{y}_1=-k_1 y_1 +\frac{1}{2}k_3(y_3+\frac{1}{2}(y_1+y_2))=(-k_1+\frac{1}{4}k_3)y_1+\frac{1}{4}k_3y_2+k_3y_3\]
\[m_2\]
: \[m_2 \ddot{y}_2=-k_2 y_2 +\frac{1}{2}k_3(y_3+\frac{1}{2}(y_1+y_2))=\frac{1}{4}k_3y_1+(-k_2 +\frac{1}{4}k_3)y_2+k_3y_3\]
\[m_3\]
: \[m_3 \ddot{y}_3=-k_3(y_3-\frac{1}{2}(y_1+y_2))=\frac{1}{2}k_3y_1+\frac{1}{2}k_3y_2-k_3y_3\]
We can divide these equations by
\[m_1, \: m_2, \: m_3\]
respectively and writing in matrix form gives us the equation\[\begin{pmatrix}\ddot{y}_1 \\ \ddot{y}_2 \\ \ddot{y}_3 \end{pmatrix} = \left( \begin{array}{ccc} \frac{-k_1+k_3/4}{m_1} & \frac{k_3}{4m_1} & \frac{k_3}{4m_1} \\ \frac{k_3}{4m_2} & \frac{-k_2 +k_3/4}{4m_2} & \frac{k_3}{m_2} \\ \frac{k_3}{2m_3} & \frac{k_3}{2m_3} & \frac{k_3}{m_3} \end{array} \right) \begin{pmatrix}y_1 \\ y_2 \\ y_3 \end{pmatrix}\]
Find the eigenvalues
\[\lambda_i\]
and the natural frequencues of the system are \[f=2 \pi \omega=2 \pi \sqrt{\lambda}\]
. 