We can find the kinetic energy that must be given to a body of mass![]() stationary at the surface of a non rotating spherically distributed mass
stationary at the surface of a non rotating spherically distributed mass![]() and radius
and radius![]() to just remove it into space far away from the body by equating the required kinetic energy to the negative of the gravitational potential energy.
to just remove it into space far away from the body by equating the required kinetic energy to the negative of the gravitational potential energy.
![]()
Hence![]() (1)
(1)
![]() is called the escape velocity. If the radial velocity of the body is greater than the escape velocity then the body will escape the gravitational influence of the mass.
is called the escape velocity. If the radial velocity of the body is greater than the escape velocity then the body will escape the gravitational influence of the mass.
We know no material particle can travel faster than the speed of light![]() and might ask 'what happens when the escape velocity reaches the speed of light?' Then v=c and not even light will escape from the surface of the body.
and might ask 'what happens when the escape velocity reaches the speed of light?' Then v=c and not even light will escape from the surface of the body.
(1) becomes![]() which can be rearranged to give the radius that a body of mass
which can be rearranged to give the radius that a body of mass![]() must be confined to so that the escape velocity equals
must be confined to so that the escape velocity equals![]() This value of
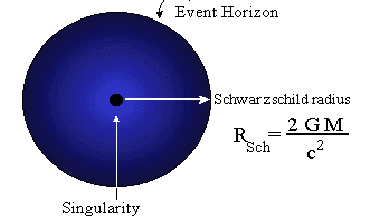
This value of![]() is called the Schwarzschild radius and labelled
is called the Schwarzschild radius and labelled![]()
Every black hole has a radius equal to it's Schwarzschild radius. The actual size of the mass in the black hole may be a great deal smaller than the Schwarzschild radius but we cannot tell, since light cannot pass from inside the black hole to outside. In fact the mass is thought to constitute a singularity at the centre of the hole, where the known laws of physics break down.