Proof of the Radius of Convergence Theorem

The Radius of Convergence Theorem

For a given power series,precisely one of the following may happen

1. the series converges only for

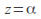
2. the series converges for all

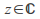
3. there is some real number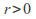such that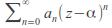converges and converges absolutely if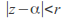and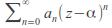diverges if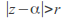

The proof rests on the claim that if a power series is convergent for someon a circle with centre the origin, then it is absolutely convergent for all points inside the circle.

Note that ifis convergent thenso that for some

Hence forand the series converges so the seriesconverges by the comparison test.

Suppose that neither 1 or 2 above hold. Consider the set

Since 1 does not hold there is somesuch thatis convergent and hence the setis not empty. Moreover,is an interval (and not a set of discrete points) sinceandthenSince 2 does not hold there is somesuch thatis divergent and henceis divergent. Thusand so the interval of convergence has a finite, non zero, right hand end point(which may or may not be in).

Ifthenis convergent henceis absolutely convergent.

On the other hand, ifthen we can chooseto satisfythenis divergent (since) henceis divergent.