Proof of the Open Mapping Theorem

The Open Mapping Theorem states:

Letbe a function analytic and non – constant on a regionand letbe an open subset ofThenis open.

Proof

To prove thatis open we need to show that ifthen there exists such that

Sincethere existssuch thatFurther, the solutions of the equationare isolated sinceis non constant and analytic and so we can find an open discinwith centreand radius sufficiently small such thatforThus, ifis a circle inwith centrethen the imageis a closed contour which does not pass through

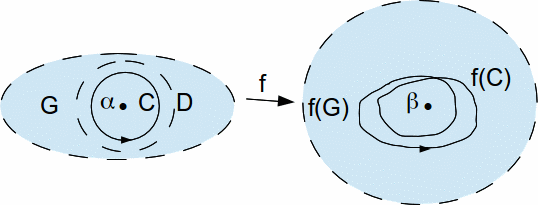
is compact, being the continuous image of a compact set, so the complement ofis open and we can chooseso that lies in the complement of

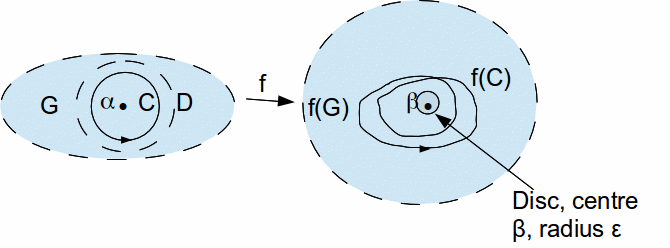
The winding number ofabout each point of the disc is equal to

Nowby the Argument Principle sinceso for

Thus by the Argument Principle again, the equationhas at least one solution inside for eachsuch thathence as required.