\[x^2=-1\]
. This equations has no solution because \[x=\sqrt{-1}\]
does not exist (you cannot take the square root of a negative number).Fro an equation
\[f(x)=c\]
to have o solution means that the curves \[y=f(x), \:y=c\]
do not intersect, or the curve \[y=f(x)-c\]
never crosses the \[x\]
- axis.Suppose
\[f(x)=x^2+x\]
and \[c=-3\]
.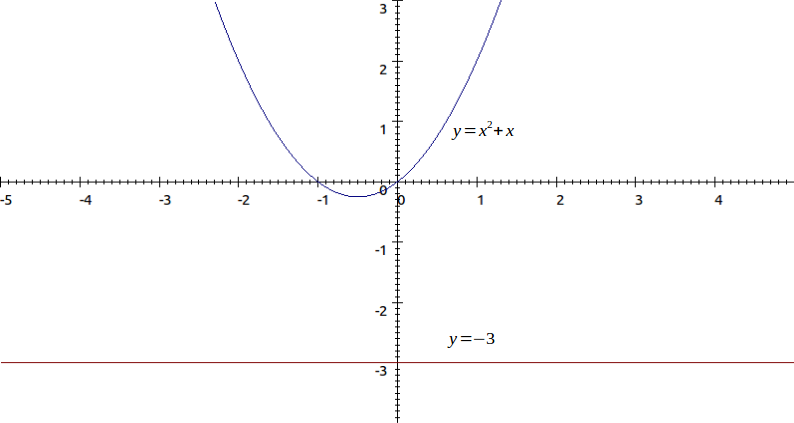
\[x^2+x=-3\]
or \[x^2+x+3=0\]
Use the quadratic formula
\[x=\frac{-b \pm\sqrt{b^2-4ac}}{2a}\]
with \[a=1, \: b=1, \: c=3\]
\[x=\frac{-1 \pm \sqrt{1^2-4 \times 1 \times 3}}{2 \times 1}=\frac{-1 \pm \sqrt{-11}}{2}\]
Since we cannot take the square root of a negative number, the equation has no solutions. Of course, we knew this because the graphs do not intersect.
