Trapezium Cut in Half By Line Parallel to Slant Height

A trapezium ABCD with parallel sides 10 and 4, and height 8 is to be cut in half parallel to a slanted side.

The result is a trapezium and a parallelogram. If the base of the parallelogram is

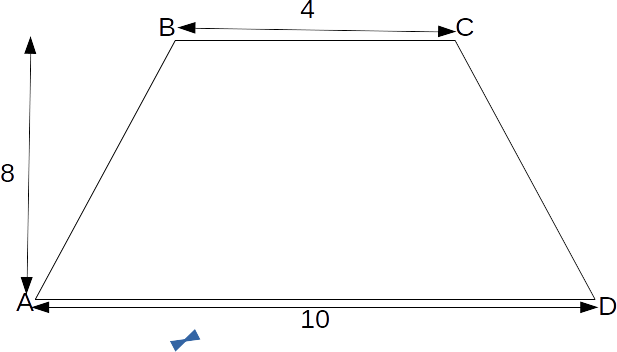
\[x\]

then the base of the smaller trapezium is

\[10-x\]

and the top side has length

\[4-x\]

.

The area of the small trapezium is

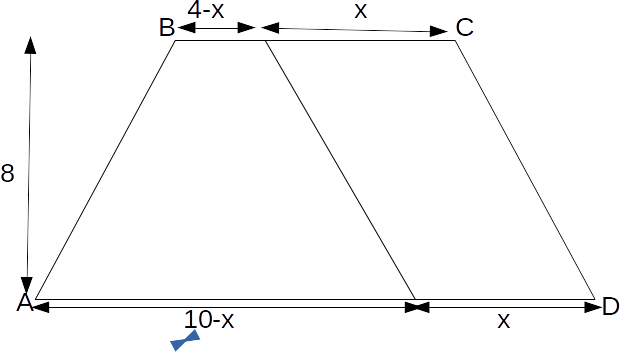
\[\frac{1}{2}(10-x+4-x) \times 8=56-8x\]

and the area of the parallelogram is

\[8x\]

.
Equating these gives

\[56-8x=8x \rightarrow 16x=56 \rightarrow x= \frac{56}{16}=3.5\]