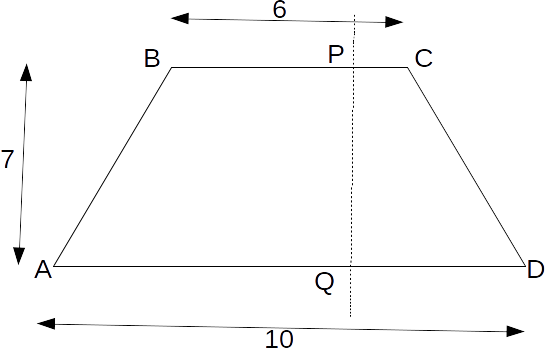
Trapezium Split in Ratio By Vertical Line

Suppose we have a trapezium

\[ABCD\]

with top and bottom sides 6 and 10 respectively, and height 7, split via a vertical line into trapeziums

\[APQD\]

and

\[PBCQ\]

that have areas in the ratio

\[2:1\]

Let

\[AP=x\]

then

\[DQ=x+2\]

.

The area of

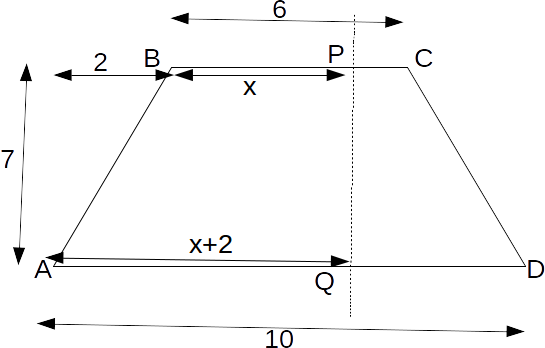
\[APQD\]

is two thirds the area of

\[ABCD\]

.
Hence

\[\frac{1}{2}(x+x+2) \times 7 =\frac{2}{3} \times \frac{1}{2}(10+6) \times 7=\frac{112}{3}\]

\[7x+7=\frac{112}{3} \rightarrow x = \frac{112/3-7}{7}= \frac{13}{3}\]