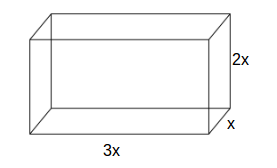
Suppose the height of a cuboid is twice its width and the length is three times its width.
If we label the with as
\[x\]
then the height is \[2x\]
and the length is \[3x\]
.
\[V=x \times 2x \times 3x=6x^3\]
.The surface area is
\[A=2(x \times 2x + x \times 3x+2x \times 3x)=22x^2 \]
.Suppise the height of a cone is twice the radius. We can write
\[h=2r\]
.
The volume of the cone is \[V=\frac{1}{3} \pi r^2 h= \frac{1}{3} \pi r^2 (2r)= \frac{2}{3} \pi r^3\]
.The surface area is
\[\begin{equation} \begin{aligned} A &= \pi r(r+\sqrt{r^2+h^2}) \\ &=\pi r (r+\sqrt{r^2+(2r)^2} ) \\ &= \pi r (r+\sqrt{5r^2}) \\ &= \pi r^2 (1+ \sqrt{5}) \end{aligned} \end{equation}\]
