Gradients and Equations of Lines

The general equation of a line may be wriiten as

(1) where m is the gradient andis the– intercept, or

whereis again the gradient.

We may be asked:

Find the equation of the line which passes through the two pointsand

we have to find the gradient

We can then use either equation (1)

in which case we have to solve forby putting on of the two points in the question into the line. Suppose we pick the first point,

so the equation of the line is

(1)

If we are also asked to express the equation of the line in the formwe can multiply (1) by 3 to clear the fractions:

then subtractfrom both sides to give:

To use the equationwe find the gradient as above then choose one of the points and substitute it into the equation asFor example, suppose we choose the first point above:

Then add 5 to both sides to obtainWe can also rearrange this into the form

as above.

We may also have to find the equation of a line from a graph. The method is shown below.

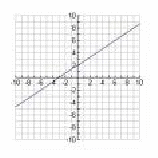
We use the equationWe can readtheintercept off the graph. It is 2. We find the gradient using

The most obvious points to pick forandare where the graph crosses the coordinate axes. These are the points andThe gradient isThe equation of the line is then