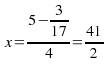Solving Simultaneous Equations Algebraically

Simultaneous equations are simultaneously true, so they have the same values of and at the same time. We can solve simultaneous equations graphically, or algebraically. I show here how to solve simultaneous equations algebraically.

We have to line up the's and's if they are not already aligned. For the above example, they are aligned.

The coefficients of the's are the same here so we can eliminate them by adding the equations termwise.

Then substitute this value ofback in to one of our original equations to find. If we choose the 1 ^st equation then

so The solution is.

The equationsand are not aligned. We align them first.

(1)

(2)

Now we choose whether to eliminate the's or the's. I choose the first. I have to make the coefficients the same and because they are both positive I subtract. I do 3*(1)-4*(2)

Subtraction givesso . Substitute this value of y into one of the original equations to find . I choose (1)

so