A point P is free to move along the
\[x\]
axis between points A and B.Line segments joint to point P to points R and S as shown, and the lines PR and PS make angles \[\theta\]
and \[\phi\]
with the positive and negative \[y\]
axes respectively. How can you find \[\frac{D \theta}{D \phi}\]
?
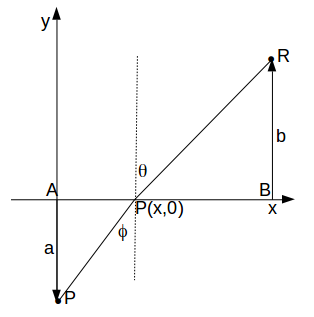
\[tan \theta =\frac{AB-x}{b} \rightarrow sec^2 \theta \frac{d \theta}{dx}=- \frac{1}{b} \rightarrow \frac{d \theta}{dx}=- \frac{cos^2 \theta}{b}\]
\[tan \phi =\frac{x}{a} \rightarrow sec^2 \phi \frac{d \phi}{dx}= \frac{1}{a} \rightarrow \frac{d \phi}{dx}= \frac{cos^2 \phi}{a}\]
Then
\[\frac{d \theta}{d \phi}=\frac{\frac{d \theta}{dx}}{\frac{d \phi}{dx}}=\frac{- \frac{cos^2 \theta}{b}}{ \frac{cos^2 \phi}{a}}=- \frac{a cos^2 \theta}{b cos^2 \phi}\]
