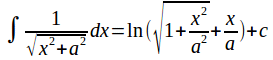The integrals of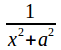 and
and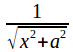 may both be evaluated by substitution. Specifically, substitute
may both be evaluated by substitution. Specifically, substitute![]()
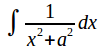
If![]() then
then
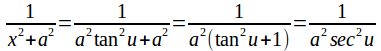
and![]()
The integral becomes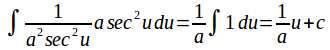
The original substitution was![]() so
so![]() and
and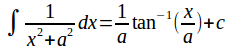
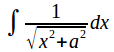
If![]() then
then
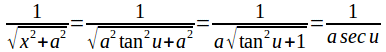
and![]() as before.
as before.
The integral becomes![]()
The original substitution was![]() so that
so that![]()
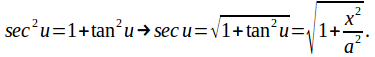
Hence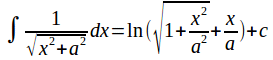
The integrals of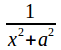 and
and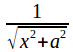 may both be evaluated by substitution. Specifically, substitute
may both be evaluated by substitution. Specifically, substitute![]()
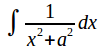
If![]() then
then
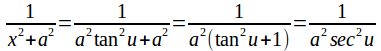
and![]()
The integral becomes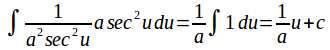
The original substitution was![]() so
so![]() and
and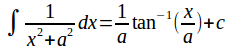
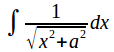
If![]() then
then
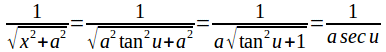
and![]() as before.
as before.
The integral becomes![]()
The original substitution was![]() so that
so that![]()
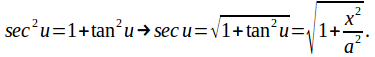
Hence