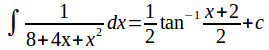If an integral can be evaluated using the substitution method, it of often simpler to make two substitutions. The first seeks to simplify the integrand into a more familiar form which.
Example:![]()
Complete the square inside the square root to obtain![]()
Now substitute![]()
![]() The integral becomes
The integral becomes
![]()
Now substitute![]()
![]() The integral becomes
The integral becomes
![]()
This can be evaluated using the trigonometric identity![]() rearranged as
rearranged as![]() We have
We have![]()
Now use the substitutions to obtain the result in terms of x. Use![]() and
and![]()
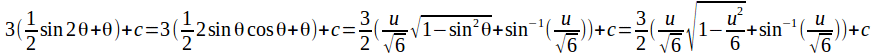 Now use u=x+1 to obtain the result
Now use u=x+1 to obtain the result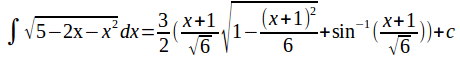
Example: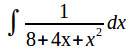
Complete the square inside the square root to obtain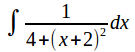
Now substitute![]()
![]() The integral becomes
The integral becomes
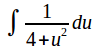
Now substitute![]()
![]() The integral becomes
The integral becomes
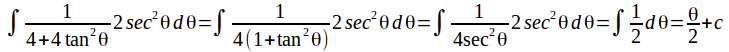
Use![]() and
and![]() successively to obtain
successively to obtain