Any equation of the form
where
and
are constants, and
and
are variables, can be transformed into a linear equation by taking logs.
Ifthen
Using the logarithm law
with
and
and natural logs gives
Using the logarithm law
(again using natural logs) with the second term on the right hand side gives
This is equation of a straight line, with x plotted against ln y .
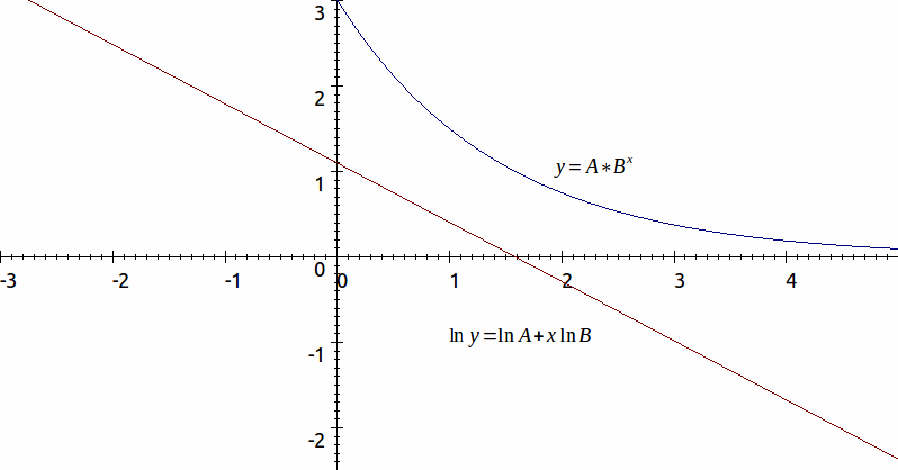
Straight line graphs are desirable because theintercept and gradient are easy to find and this allows the constants of the original exponential equation to be found.
The– intercept of the straight line graph above is 1.1
so
to 1 decimal place.
The gradient of the graph is
to 2 decimal places so
to two decimal places.
Then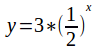
to within the limits of our graph.