Disproving a statement is often simpler than a proof. Finding a counterexample will often suffice. Since a statement cannot be both true and false, if you find a counterexample, the statement must be false.
Example: If![]() then
then![]()
This statement is 'obviously true', but if![]() and
and![]() then
then![]() but
but![]() so the statement is not true.
so the statement is not true.
If![]() and
and![]() are both greater than or equal to zero then the statement is true.
are both greater than or equal to zero then the statement is true.
Formally, if![]() and
and![]() then
then![]()
Example: If![]() then
then![]()
Again the statement is true if only positive numbers are considered – it is also true if only negative numbers are considered. If one number is negative and the other is positive then the statement is false.
Take![]() and
and![]() then
then![]() but
but![]()
Example: If![]() and
and![]() are different irrational numbers, then
are different irrational numbers, then![]() and
and![]() are both irrational.
are both irrational.
Take![]() and
and![]() so that
so that![]() and
and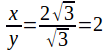 so that
so that![]() and
and![]() are both rational.
are both rational.
Example: If![]() and
and![]() are different irrational numbers, then
are different irrational numbers, then![]() and
and![]() are both irrational.
are both irrational.
Take![]() and
and![]() so that
so that![]() and
and![]() so that
so that![]() and
and![]() are both rational.
are both rational.
