Peridic functions are extremely important. Many circular motions are periodic, as are many sums of trigonometric functions.
Motion in a circle with constant speed can be written in Cartesian form as
where
is the radius of rotation and the amplitude of the vibration projected onto the x or y axes.
Any function of the form
is also periodic. We can write
where
and
if
and
if 
If the motion of a particle is described by a functionthen the motion is periodic with amplitude A, period
and phase
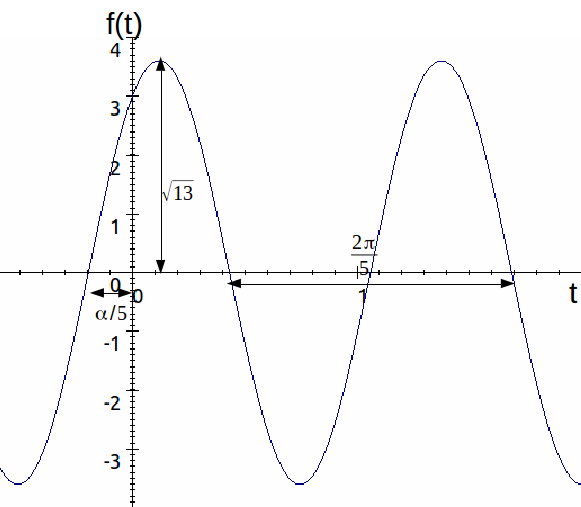
Example:
We can write it as
where
The amplitude of the motion is
the period is
and the phase isThe motion of the particle is shown below.
