Interior and Exterior Periodic Points of Basic Quadratic Functions

The nature of periodic points – such thatfor someso that repeated applications ofeventually return the value- fordepends on whether the point is an interior or boundary point of the keep setof

Ifis attracting thenis an interior point of

Ifis repelling thenis a boundary point of

Proof

Suppose thatis an attracting periodic point ofwith periodThenis an attracting fixed point ofhence there is an open disc with centrewhose points are attracted tounder repeated applications ofThese points do not escape to infinity under iteration byso lie inandis an interior fixed point of

Next suppose thatis a repelling fixed point so thatand

Sincewe must show thatis not an interior point ofIf it were an interior point then we could choose an open disclying inso thatforand

andforand(1)

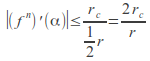Now apply Cauchy's Estimate to each polynomialto deduce thatfor

By the Chain Rule

sinceis a fixed point ofso the sequences tend to infinity, contrary to (1) so

A similar argument applies ifis a repelling periodic point ofwith period