Integrating the Gamma Function Around a Contour

The Gamma functionis not analytic onbut has simple poles at

The residues at each of these points is

Suppose then that we want to evaluate the integral ofaround the contour consisting of the circleshown below.

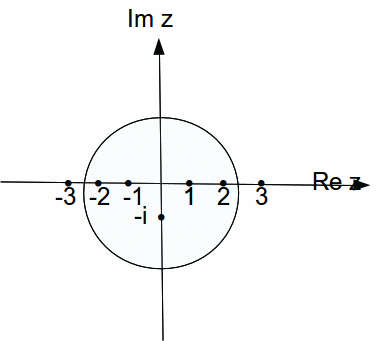
The distance from -1 to -i isand the distance from -2 to -i isso both these points are inside the circle. Of course the origin is inside the circle.

According to Cauchy's Residue Theorem, the integral ofaround the circle is