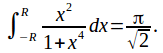If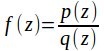
where
and
are polynomials with the degree ofat least two more than the degree of
andhas only simple, non real poles then we can find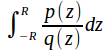
using the contour integral below.
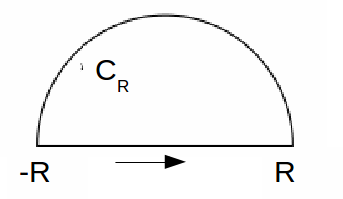
In the diagram above
is the semicircular contour of radius
By Cauchy's integral formula
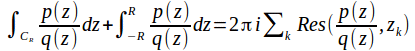where the
are the simple poles of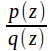
in the upper half plane.
By Jordan's Lemma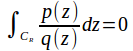
so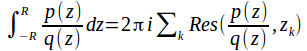
Example: Find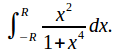
Consider the integral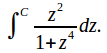
(The two integrals have the same value since both are evaluated along the real axis).
The degree of the denominator is at least two more than the degree of the numerator so we can use Jordan's Lemma.
The zeroes of
are are
and
are in the upper half plane so we evaluate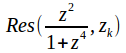
at these points.
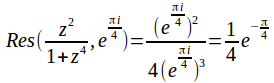and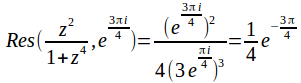 
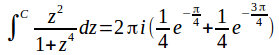
We can simplify this: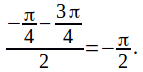
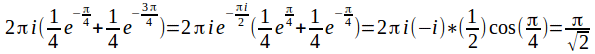
Hence