Inverse Points and Apollonian Form

An curve expressed asis said to be written in Apollonian form. A curve written in Apollonian form is in fact either a circle or a line – circles and lines together constitute the set of generalized circles, with a line being considered a circle of infinite radius.

Ifthe curve is a line. The line consists of the set of points equidistant fromand %beta .andare mirror images or inverse points of each other in the between them.

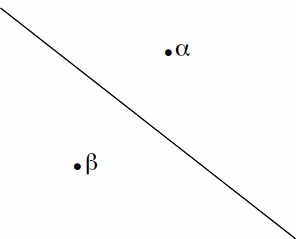
We can generalized inverse points to the case

Definition

Letbe a generalized circle.andare inverse points with respect toifand lie onandhas the equationor one of the points, say, is infinity andhas the equationfor some

Proof

Suppose thatandare distinct inverse points with respect to a generalized circleThen there exists an extended mobius transformationthat mapsto 0,to infinity andto the unit circle. Letbe the point onsatisfying

mapsonto the unit circle so so forand

Ifthis becomesso that

Ifthenso thatso that

Conversely ifhas equationwiththenand we can defineand ifhas equationandthen we can define

In either casemapsto 0,to infinity andto the unit circle since soandare inverse points with respect to