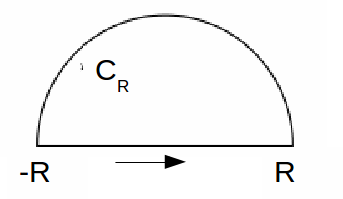
Jordan’s Lemma describes the behaviour of a contour integral on the semicircular arc or radius
(excluding the real axis) in the upper half of the complex plane as the radius of the semicircle tends to infinity.
Jordan's Lemma
If the only singularities of F(z) are simple and
as
then
if
and |F (z)| → 0 as R → ∞.
Proof: Since
is the semi-circle
and
Now
in the upper half plane, and
tends to zero faster than any power of R increases if
so by splitting the semicircular contour into three parts,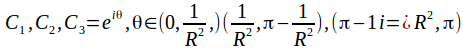
we obtain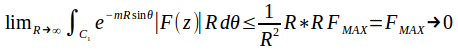
andd similarly for
and for
since as stated,
tends to 0 faster than any power ofincreases as rightarrow infinity , so
When
if
or a rational function of
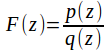with the degree of the denominator higher than the degree of the numerator can all be used.
If
then a modification is needed. The degree of the denominator must be at least two greater than the degree of the nureator.
If
then we can still apply the Lemma by taking our contour in the lower half plane.