Julia Sets

The Julia set of a quadratic functionis the boundary of the keep setor the boundary of the escape setand separates the points which escape to infinity under repeated iteration byand those which don't. The Julia set contains all the periodic repelling points ofand is the smallest closed set which contains all the repelling periodic periodic points of f. Two are illustrated below.

The Julia set has the following properties:

1. For each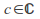the Julia set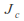is a non empty compact subset of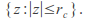

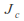2. is completely invariant.

3. 

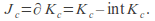
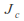4. is symmetric under rotation by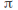about 0.

The Julia set is often plotted using the following method. Ifthen the solutions ofalso lie inThe solution areso backwards iteration gives two new points ofanditerating backwards again with these two points gives four new pointsandIterating backwards repeatedly gives more points. It can be shown that the Julia set is the smallest closed set containing all the backwards iterates of any given point ofBecause of the amount of calculation involved, not all the backwards iterates are calculated at each stage. A single iterate from each stage may be randomly selected at the backwards iterates found for that point.