\[\alpha = 36^o\]
.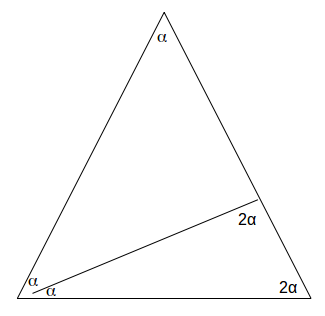
\[\alpha\]
. They are congruent triangles.Let
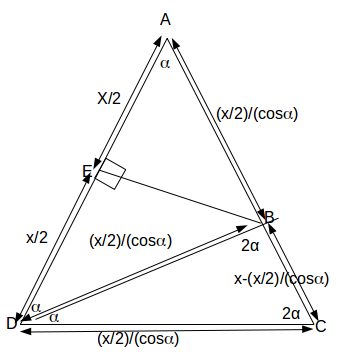
\[AC=AD=x\]
then \[AE=ED=x/2\]
.Using trigonometry on triangle
\[ABE\]
gives \[AB=\frac{x/2}{cos \alpha}\]
then \[CB=\frac{x/2}{cos \alpha}\]
too.From triangle
\[BCD\]
with \[\alpha=36^o\]
, \[\angle DBC=180^o-3 \times 36=72^o=2 \alpha\]
.Then triangle
\[BCD\]
is isosceles and \[CD=\frac{x/2}{cos \alpha}\]
.Also,
\[CD=x-\frac{x/2}{cos \alpha}\]
.
\[BCD\]
.
\[(x-\frac{x/2}{cos \alpha})^2=(\frac{x/2}{cos \alpha})^2+(\frac{x/2}{cos \alpha})^2-2(\frac{x/2}{cos \alpha})(\frac{x/2}{cos \alpha})^2 cos \alpha\]
Expanding the brackets, Dividing by
\[x^2\]
and multiplying by \[4cos^2 \alpha\]
gives\[4cos^2 \alpha-4cos \alpha +1=2-2cos \alpha \rightarrow 4cos^2 \alpha-2 cos \alpha-1=0\]
The from the quadratic formula \[cos \alpha=\frac{--2 \pm \sqrt{20}}{2 \times 4}= \frac{1 + \sqrt{5}}{4}\]
.We ignore the minus option because this returns a negative value for
\[cos \alpha\]
but \[cos \alpha \gt 0\]
. 