\[x\]
in the problem below.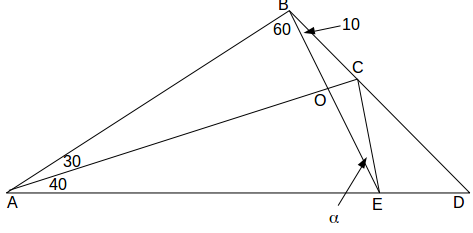
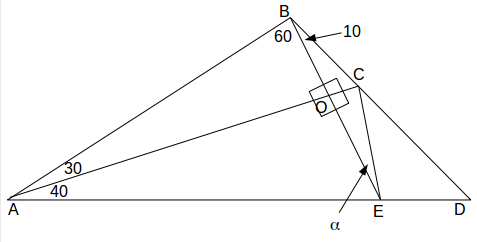
\[OAB+ABO=90^o \rightarrow AOB=90^0\]
and in fact all the angles at \[O\]
are right angles. Let \[A)=x\]
.
\[EO=x tan40, \: BO=xtan30, \: OC=(xtan30)tan10\]
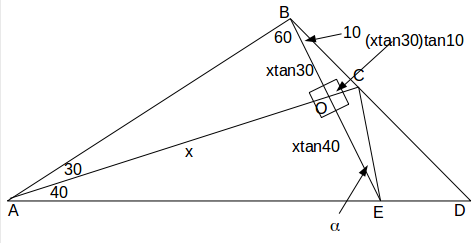
\[tan \alpha = \frac{(xtan30)tan10}{tan40}=0.1213 \rightarrow \alpha= tan^{-1}(0.1213)=6.92^o\]
. 