\[2r\]
is a circle radius \[r\]
as shown. P is a fixed point on the circumference of the smaller circle. 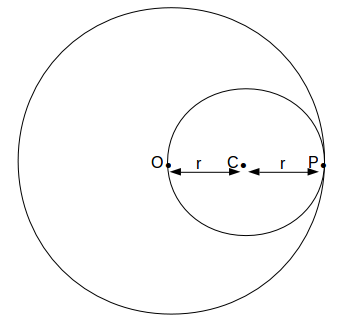
\[L=2 \pi (2r)=4 \pi r\]
so will turn about an angle \[\frac{4 \pi r}{r}= 4 \pi\]
about its centre. In fact the small circle turns about its own centre through twice the angle that it turns about the centre of the large circle.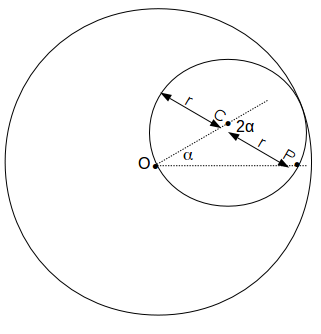
\[(rcos \alpha + r cos \alpha , rsin \alpha - r sin \alpha )=(2r cos \alpha , 0)\]
.Hence the
\[y\]
coordinate of P is constant and the point P remains on the \[x\]
axis.
