\[Dm\]
away.
If the girl measures the angle between the top and bottom of the window to be 30o, what is \[D\]
?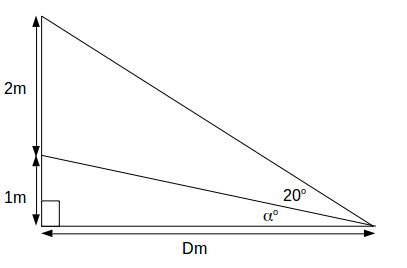
\[\alpha\]
and \[tan \alpha = \frac{1}{D} \rightarrow D=\frac{1}{tan \alpha}\]
.The angle subtended by the bottom 1m of wall and the window is
\[\alpha + 30\]
and \[tan ( \alpha +30) = \frac{3}{D} \rightarrow D=\frac{3}{tan ( \alpha + 30)}\]
.Hence
\[\frac{1}{tan \alpha} = \frac{3}{tan ( \alpha + 30)} \rightarrow 3tan \alpha =tan (\alpha + 30)=\frac{tan \alpha + tan 30}{1-tan \alpha tan 30}= \frac{tan \alpha + 1/\sqrt{3}}{1-tan \alpha / \sqrt{3}}\]
Multiplying top and bottom by
\[\sqrt{3}\]
gives \[3tan \alpha = \frac{\sqrt{3} tan \alpha +1}{\sqrt{3} - tan \alpha}\]
.Now multiply both sides by
\[\sqrt{3} - tan \alpha\]
to give \[3tan \alpha (\sqrt{3} - tan \alpha=\sqrt{3} tan \alpha +1\]
.Rearrangement gives
\[3 tan^2 \alpha - 2 \sqrt{3} tan \alpha +1 =0 \rightarrow (\sqrt{3} tan \alpha -1)^2 =0 \rightarrow \alpha = tan^{-1}(1/ \sqrt{3}) = 30^o\]
. 