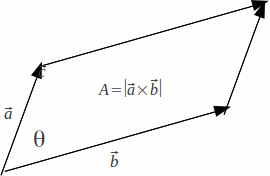
If a parallelogram is defined by two vectors
and
then the area of the parallelogram is defined by
( Note
where
is the angle betweenand
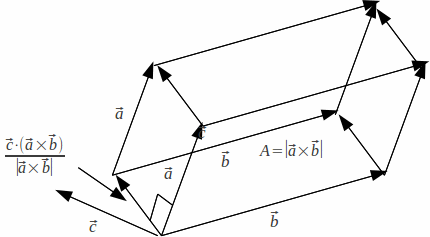
If the vectorsand
are joined by a third vector
to form a solid shape, then the volume of the solid is the area of the base (which we may consider to be the area of the parallelepiped formed byand) multiplied by the height.
is perpendicular to bothandso is in the direction of the vertical height. By taking the dot product ofwithand dividing by
we obtain the component ofperpendicular to
This is the height of the parallelpiped. Multiplying bygives the volume: This is illustrated below.
If the vectors
are in the same plane, then they are linearly dependent, since three vectors in a two dimensional space are linearly dependent. They all lie in the same plane and the height of the parallelepiped is zero. If a matrix is formed with the columns or rows consisting of the three vectors, the determinant of this matrix will be zero since the vectors are linearly dependent.