There are two well known and familiar equations for the resistance in a circuit:
![]() (1) for resistances in series
(1) for resistances in series
Proof:
![]()
The current in each resistor is the same -![]() - and the voltage across each resistor adds to the total voltage across the two resistors -
- and the voltage across each resistor adds to the total voltage across the two resistors -![]() Use the equation
Use the equation![]() for each resistance individually and the whole circuit to get,
for each resistance individually and the whole circuit to get,
![]() and divide by the common factor
and divide by the common factor![]() to get
to get![]()
and![]() (2) for resistances in parallel.
(2) for resistances in parallel.
Proof:
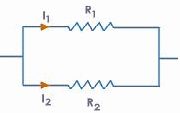
The voltage across each resistor is the same -![]() - and the current through each resistor adds to the total current through the two resistors -
- and the current through each resistor adds to the total current through the two resistors -![]() Use the equation
Use the equation![]() for each resistance individually and the whole circuit to get,
for each resistance individually and the whole circuit to get,
![]() and divide by the common factor
and divide by the common factor![]() to get
to get![]()
More fundamental however is the equation![]() (3) which introduces the resistivity
(3) which introduces the resistivity
![]() of a material. The resistivity is a fundamental property of the material, ranging from
of a material. The resistivity is a fundamental property of the material, ranging from![]() for a conductor like silver to
for a conductor like silver to![]() for a resistor like wood.
for a resistor like wood.
The resistivity equation (3) is in fact a consequence of the other two, since having two resistances in series is equivalent two having twice the length of wire, so we may say:
Resistance is directly proportional to length.
The equation for two identical resistances in parallel implies that two resistances in parallel halves the total resistance. This is equivalent to doubling the cross sectional area. This implies that the resistance is inversely proportional to the area. We may write down the equation:
![]() where K is a constant of proportionality which we call the resistivity and label
where K is a constant of proportionality which we call the resistivity and label![]()
