\[2x\]
. Draw a line from the centre of the circle - which is also the centre of the triangles - to a vertex of the triangle as shown.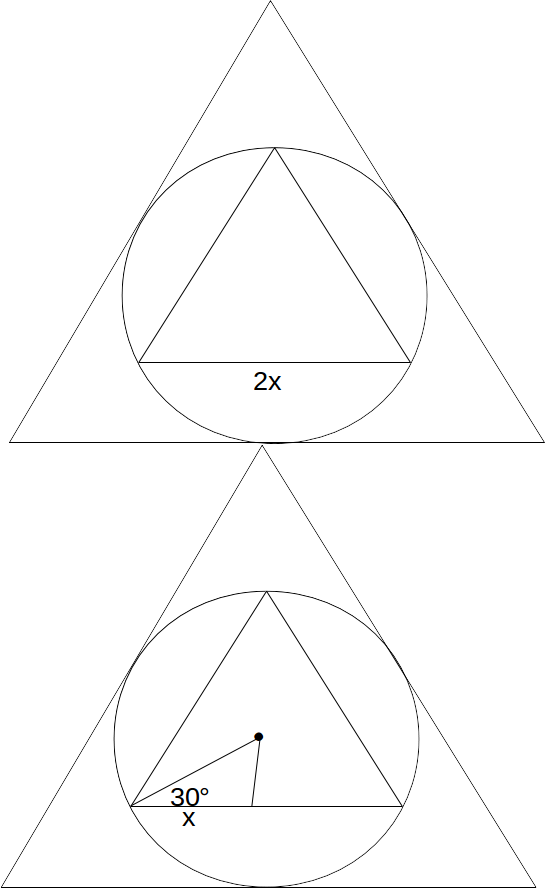
\[cos 30 = \frac{x}{r} \rightarrow r= \frac{x}{cos 30}= \frac{x}{2/ \sqrt{3}} = \frac{2x}{ \sqrt{3}}\]
Now drop a line from the centre of the circle to the centre of the base of the large triangle to form a right angle triangle as show. We use simple trigonometry to find the base of the;large triangle.
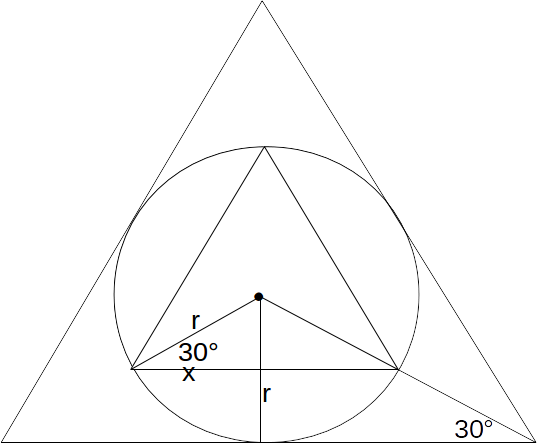
\[tan 30 = \frac{r}{half \: the \: base} \rightarrow base =\frac{r}{1/2 tan 30}= \frac{2x / \sqrt{3}}{1/2 \times 1 / \sqrt{3}}= 4x\]
Then sides of the big triangle are
\[\frac{4x}{2x} = 2\]
times the sides of the small triangle and the are of the big triangle is the square of this ( equals 4) times the area of the small triangle.