\[r\]
.
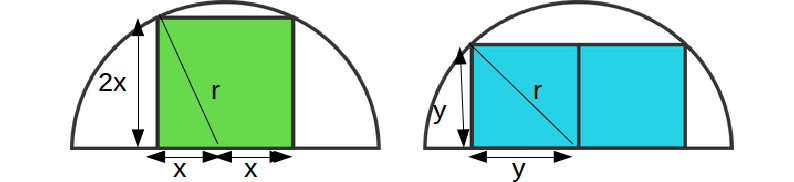
\[x\]
then from the diagram,
\[(2x)^2+x^2=5x^2=r^2 \rightarrow x = \frac{r}{\sqrt{5}}\]
.The area of the square is
\[(2 \frac{r}{\sqrt{5}})^2 = \frac{4r^2}{5}\]
.For the square on the right, of side
\[y\]
\[y^2+y^2=2y^2 =r^2 \rightarrow y = \frac{r}{\sqrt{2}}\]
.The area of the two squares is
\[2 \times (\frac{r}{\sqrt{2}})^2 =r^2\]
.The ratio of the areas is
\[\frac{4r^2}{5} : r^2\]
which simplifies to \[4:5\]
.