\[r_1, \: r_2\]
.
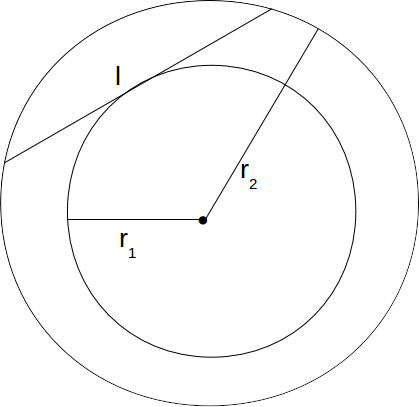
\[l\]
which just touches the outer circle. To find the length of this line in terms of \[r_1, \: r_2\]
complete the triangle using the line and two radii of the large circle as shown. Draw a line from the centre of the circle bisecting the tangent and label the angles between the radii as \[\theta\]
.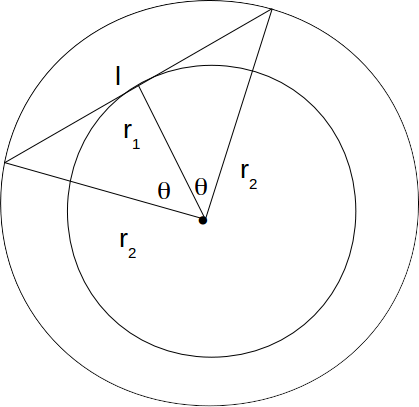
\[cos \theta = \frac{r_1}{r_2} \]
.The angle subtended at the centre of the circle by the tangent is
\[2 \theta\]
.\[cos 2\theta =2 cos^2 \theta -1 =2 ( \frac{r_1}{r_2})^2 -1\]
.Now use the Cosine Rule to find the length of the tangent.
\[\begin{equation} \begin{aligned} l^2 &= r_2^2+r_2^2-2 r_2^2 cos 2 \theta \\ & =2r_2^2 -2r_2^2 (2( \frac{r_1}{r_2})^2 -1) \\ &= 4r_2^2-4r_1^2 \end{aligned} \end{equation} \]
.Then
\[l= \sqrt{4r_2^2-4r_1^2}= 2 \sqrt{r_2^2-r_1^2}\]
