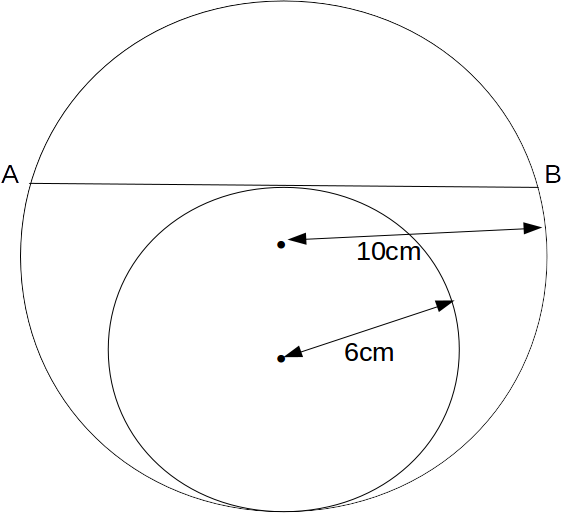
Suppose we have a small circle inside a larger circle, the circles touching tangentially at the bottom, A horizontal line is dr awn tangentially to the small circle to meet the large circle. What is the length of this line?
Label the centre of the large circle as O. From the centre of the large circle draw a vertical line to meet the horizontal line at C. The triangle OCB is a right angled triangle, and OC=x=12-10=2cm.
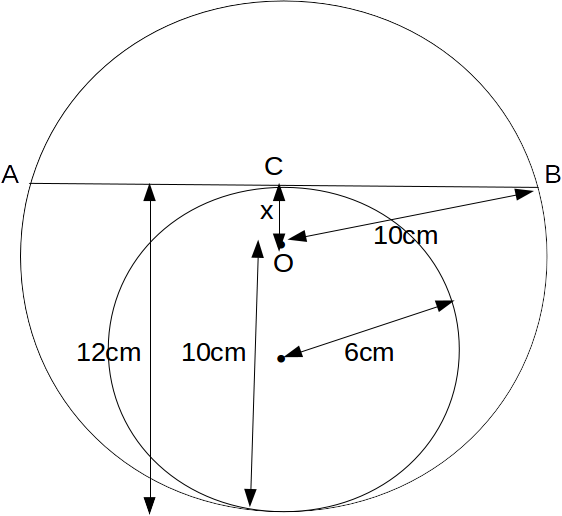
Then
\[CB=\sqrt{10^2-2^2}=\sqrt{96}=\sqrt{16} \sqrt{6}=4 \sqrt{6}cm\]
.
Then
\[AB=2CB=8 \sqrt{6}cm\]



