\[V= \frac{1}{3}Base \: Area \times Height\]
The diagram shows a trapezium with sides of length
\[2x\]
.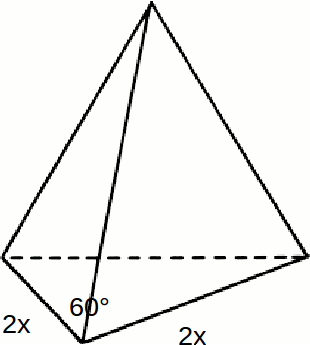
\[\frac{1}{2} 2x \times 2x \times sin 60=x^2 \sqrt{3}\]
To find the height, first find the distance from a vertex of the base to the centre of the base. Divide the base into three equal triangles by drawing lines from the centre to the vertices. The triangle formed with have an angle of 120 degrees opposite a side of
\[2x\]
.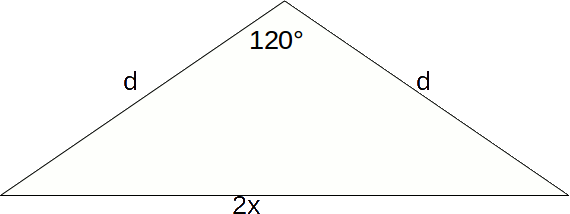
\[(2x)^2=d^2+d^2-2d \times d \times cos 120=2d^2-2d^2 \times - \frac{1}{2} = 3d^2 \rightarrow d = \frac{2x}{\sqrt{3}}\]
Now form the right angled triangle as shown and use Pythagoras Theorem to find the height.
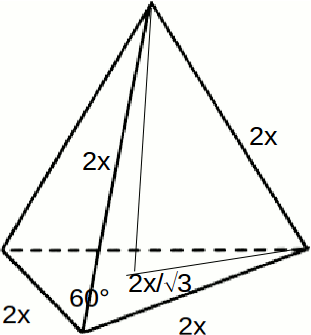
\[\sqrt{(2x)^2 - (\frac{2x}{\sqrt{3}})^2}= \frac{2x \sqrt{2}}{\sqrt{3}}\]
The volume is then
\[\frac{1}{3} Base \: Area \times Height = \frac{1}{3} \times x^2 \sqrt{3} \times \frac{2x \sqrt{2}}{\sqrt{3}} = \frac{2x^3 \sqrt{2}}{3}\]
