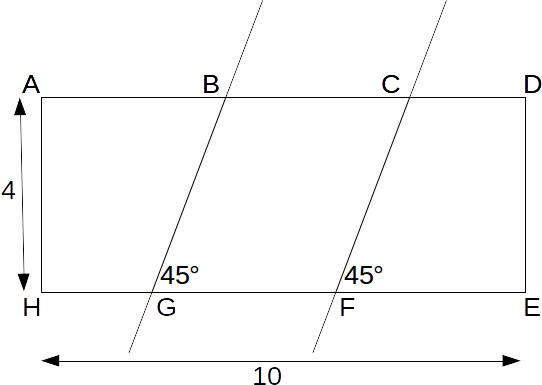
Suppose we have a rectangle cut into three by two parallel lines BG and CF making an angle of 45° with EG as shown. The areas of the three shapes formed are equal, so that the area of ABGH, BCFG and CDEF are equal. What must the length of HG be so that this is so?
Draw a vertical line from G to the top side at P

then
\[tan 45=\frac{PB}{PG} \rightarrow 1=\frac{PB}{4}\rightarrow PB=4\]
Then
\[AB=x+4\]
By syymetry,
\[EF=x+4\]
and then
\[FG=10-(x+x+4)=6-2x\]
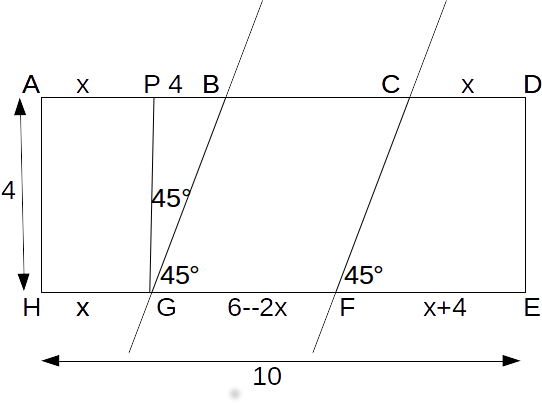
The areas of ABGH and BCFG are equal.
\[\frac{1}{2}(x+x+4)(4)=(6-2x)(4) \rightarrow x+2=6-2x \rightarrow 3x=3x=4 \rightarrow x=\frac{4}{3}\]





