We often need to find the potential at each point in a region of space due to a distribution of charges. We start at Gauss's Law![]() (1)
(1)
The electric field is given in terms of the potential![]() by
by![]() and we can substitute this into (1) to obtain
and we can substitute this into (1) to obtain![]() (2)
(2)
The combination div grad is known as the Laplacian operator and written![]() It is a second order differential operator. In Cartesian coordinates it takes the form
It is a second order differential operator. In Cartesian coordinates it takes the form![]() and substituting this into (2) gives
and substituting this into (2) gives![]()
This equation is known as Poisson's equation.
The problem of finding the potential of a distribution of charges is now reduced to finding the solution to a second order differential equation. Many distributions involve some sort of symmetry or uniformity.
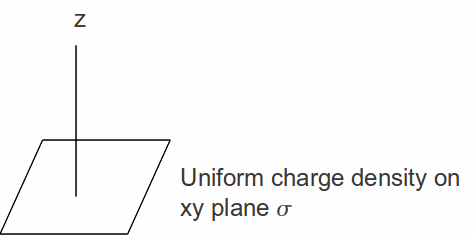
Charge may be distributed uniformly on a plate and we need to find the potential at a distance from the plate. There is symmetry in the xy plane.
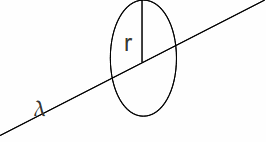
or on a thin long wire and we need to find the potential at a radial distance r. There is radial symmetry.
Obviously a point charge or chage distribution on the surface of a sphere have spherical symmetry. By using appropriate coordinater systems for each case of symmmetry, the Poisson equation can be quickly solved.
