Cayley's Theorem
Cayley's Theorem
If
is a group of order
thenis isomorphic to a subgroup of the permutation group
Example: Letbe the Klein group
of order 4,
with every element self inverse, so of order 2.
Example: We can define
then
is an isomorphism fromonto 
Proof of Cayley's Theorem
Let the
elements ofbe
For an element
we find the permutation of the elements offormed by multiplying each element on the left by
Each
must be equal to
for some
if and only if
We must show
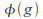is a uniquely defined element of
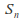for each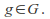
- is one to one.
- has the morphism property,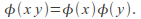
By constructionmaps the set
to itself.is one to one since if
and 
then
and
and 2 is proved. Hence is a one to one map of the set
to itself , so is a permutation of this set and
so 1 is satisfied.
To show 3, we show that
and
have the same effect on each of the elements in
Assume
and
so that
By the definition of
if and only if
andif and only if
by associativity in
but
if and only if
for each
henceandhave the same effect on every element of
so
and Cayley's Theorem is proved.
