A closed set
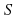
is a set that includes all it's limit points
This means than for each point
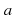
such that there exists a sequence
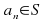
such that
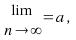
we must have that
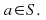
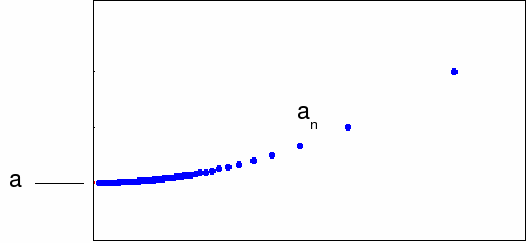
This means that the boundary of
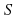
is in
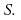
If the set does not include any of it's boundary then it is said to be open. The interval
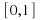
is closed, and the interval
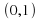
is open since the boundary of
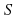
is

but
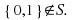
The interval
\[(0,1]\]
is neither open or closed since
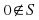
but
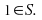
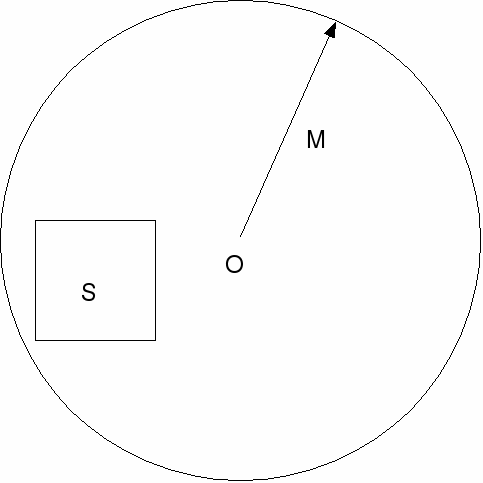
A set
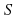
is bounded if and only if there exists
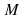
such that for all
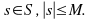
This means that the distance however measured from the origin to any element of
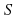
is less than or equal to
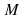
as shown below.
Finally a set is compact if it is both closed and bounded. Compactness has many applications in analysis.



