\[F\]
of sets, we can find its ZDD as follows.\[F = \emptyset\]
(\[F\]
is empty) return \[\bot\]
.
If \[F = \epsilon\]
(\[F\]
contains
only the empty set) then return \[\top\]
.
\[v\]
amongst all elements in all sets of \[F\]
.
Create a node \[v\]
.
\[F_0\]
be the family of all sets in \[F\]
not containing \[v(\]
, that is,
\[; F_0 = \{ \alpha : \alpha \in F, v \notin \alpha \}\]
.
Recursively construct the ZDD for \[F_0(\]
, and connect the LO edge from \[v\]
to
the root of \[F_0\]
.
\[F_1\]
be the family resulting from taking all sets in \[F\]
that contain
\[v\]
and then removing \[v\]
from each set:
\[ F_1 = \{ \alpha\setminus\{v\} : \alpha \in F, v \in \alpha \} \]
.
Recursively construct the ZDD for \[F_1\]
, and connect the HI edge from \[v\]
to
the root of \[F_1\]
.
\[n\]
, consider for example
the family of all sets of size \[k\]
which we denote \[S_k(\{1,...,n\})\]
. The
ZDD of \[S_2(\{1,2,3\}) = \{ \{1,2\}, \{2,3\}, \{1,3\}\}\]
is the following: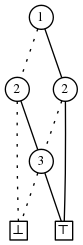
\[S_k(\{1,...,n\})\]
turns out to be easy to describe (exercise).Here are some more examples. Let
\[U = \{1, ..., 6\}\]
and \[S = \{2,3,5\}\]
.
The ZDD of all subsets of \[U\]
containing exactly one element of \[S\]
is: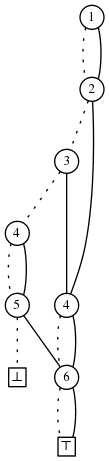
\[S\]
is:
\[S\]
is: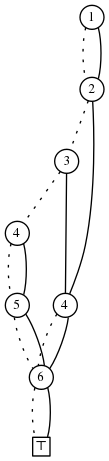
\[S(\]
, before
joining the main branch again after the largest element of \[S\]
has been handled.