A Cayley table for a group is essentially the ``multiplication table'' of the group. The columns and rows of the table (or matrix) are labelled with the elements of the group, and the cells represent the result of applying the group operation to the row-th and column-th elements. The Cayley table is square with as many rows as columns, since each element appears once along the top and down the left hand side. If the group has order n, the Cayley table has n^2 entries.
Formally, let G be our group, with operation the group operation. Let C be the Cayley table for the group, with![]() denoting the element at row
denoting the element at row![]() and column
and column![]() which is the result of applying element
which is the result of applying element![]() with
with![]()
Example: The Cayley table for the group![]() is shown below.
is shown below.
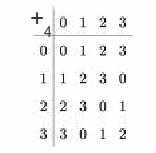
The group has elements (0,1,2,3,4). Each element appears once along the top row and down the left hand side, and once in the body of the table. The identity element 0 is symmetrically distrubuted, and this is so whether the group is Abelian so that![]() or non – Abelian
or non – Abelian![]() The above group is Abelian so the whole table is symmetric. The Cayley table for
The above group is Abelian so the whole table is symmetric. The Cayley table for![]() the group of symmetries of a square is shown below.
the group of symmetries of a square is shown below.
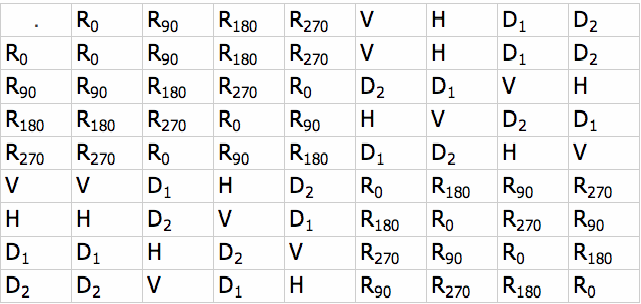
All Cayley tables for isomorphic groups are isomorphic (that is, the same, invariant of the labeling and ordering of group elements).
It has all of the features of the first table with the exception of being symmetric.![]() is non – Abelian so the Cayley table is not symmetric.
is non – Abelian so the Cayley table is not symmetric.
