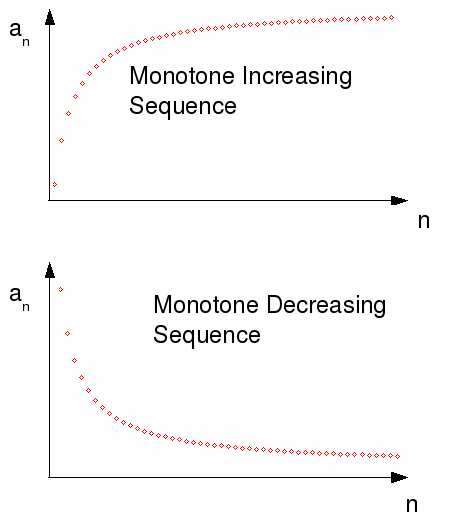
A monotone sequence is either increasing so that if![]() then
then![]() or decreasing so that if
or decreasing so that if![]() then
then![]() We make this rigorous in the following definition.
We make this rigorous in the following definition.
Definition A sequence![]() is increasing if and only if
is increasing if and only if![]() for all positive integers
for all positive integers![]() A sequence
A sequence![]() is decreasing if
is decreasing if![]() for all positive integers
for all positive integers![]() A sequence is monotone if and only if it is either increasing or decreasing.
A sequence is monotone if and only if it is either increasing or decreasing.
Theorem
A monotone sequence is convergent if and only if it is bounded.
Proof: Suppose![]() is a monotone sequence that is increasing and bounded above, then
is a monotone sequence that is increasing and bounded above, then![]() is bounded above so let
is bounded above so let![]() Choose
Choose![]() then since
then since![]() is the least upper bound of
is the least upper bound of![]()
![]() is not an upper bound, so there is no such
is not an upper bound, so there is no such![]() such that
such that![]() hence
hence![]() converges to
converges to![]()
Suppose![]() is a monotone sequence that is decreasing and bounded below, then
is a monotone sequence that is decreasing and bounded below, then![]() is bounded below so let
is bounded below so let![]() Choose
Choose![]() then since
then since![]() is the greatest lower bound of
is the greatest lower bound of![]()
![]() is not a lower bound, so there is no
is not a lower bound, so there is no![]() such that
such that![]() For
For![]() hence
hence![]() converges to
converges to![]()
