The Harmonic series is the infinite series whose sum is given by
![]()
The harmonic series diverges. This is quite easy to prove.
![]()
![]()
Thus![]() is unbounded so
is unbounded so![]() is divergent.
is divergent.
In fact![]() is in many cases divergent for many
is in many cases divergent for many![]() for example if
for example if
S is the set of prime numbers
S is the set of multiples of any number.
The series diverges very slowly. For example, the sum of the first![]() terms is less than 100. This is because the partial sums of the series have logarithmic growth:
terms is less than 100. This is because the partial sums of the series have logarithmic growth:
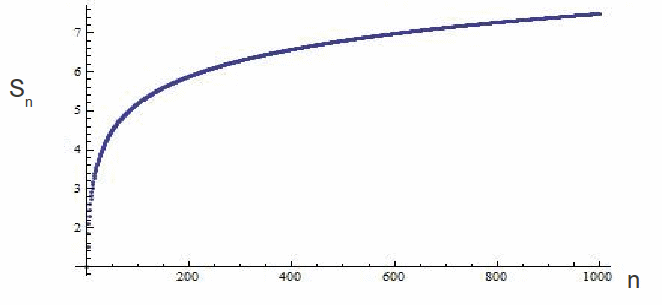
![]() as can easy be proved using the integral test.
as can easy be proved using the integral test.
