Suppose![]() is one to one, then there is a unique function
is one to one, then there is a unique function![]() such that
such that![]() for each
for each![]() and
and![]() for each
for each![]() In fact, if
In fact, if![]() is continuous then
is continuous then![]() is continuous and vice versa, if
is continuous and vice versa, if![]() and
and![]() are compact.
are compact.
Theorem Suppose![]() is continuous and one to one with
is continuous and one to one with![]() compact. Then
compact. Then![]() is continuous.
is continuous.
Proof: Let![]() be any sequence in
be any sequence in![]() converging to
converging to![]() We must show that
We must show that![]() converges to
converges to![]() Write
Write![]() for each
for each![]() then
then![]() Since
Since![]() is compact, the sequence
is compact, the sequence![]() is bounded. Let
is bounded. Let![]() be any convergent subsequence of
be any convergent subsequence of![]() with limit
with limit![]() since
since![]() is closed, and so
is closed, and so![]() is continuous at l, thus
is continuous at l, thus![]() converges to
converges to![]() but
but![]() is a subsequence of
is a subsequence of![]() hence converges to
hence converges to![]() Since
Since![]() is one to one and
is one to one and![]() Every convergent subsequence of
Every convergent subsequence of![]() converges to the same limit l so
converges to the same limit l so![]() converges to
converges to![]() and so
and so![]() is continuous at
is continuous at![]()
We must have that![]() is compact, for a reason illustrated by the example below.
is compact, for a reason illustrated by the example below.
Let![]()
![]() illustrated below, is one to one and continuous on
illustrated below, is one to one and continuous on![]()
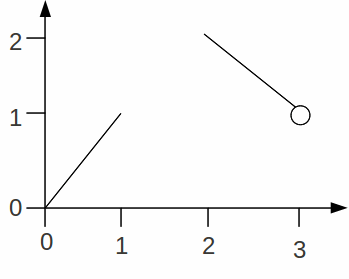
The graph of![]() is shown below.
is shown below.

Consider the sequence![]() which converges to 1. For n odd,
which converges to 1. For n odd,![]() and for
and for![]() even
even![]() so
so![]() does not converge.
does not converge.
