The Inverse Function Rule

Ifis continuous and one to one on an intervalthenexists and is continuous. Ifis differentiable then the following theorem is applicable:

Theorem

Supposeis continuous and differentiable withfor allThenis one to one,is continuous and differentiable onandfor all

Proof: Sincefor allthenis one to one.

Suppose that–is continuous sois a closed interval. Chooseand any sequence inconverging toLet foris continuous sois continuous andconverges to and sinceis one to onefor allSinceis differentiableconverges toand sinceis one to one forHenceconverges toThusis differentiable and

Example

andso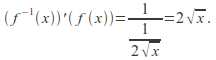

Example

andso