The Inverse Function Theorem

Supposeis one to one, then there is a unique functionsuch thatfor eachandfor eachIn fact, ifis continuous thenis continuous and vice versa, ifandare compact.

Theorem Supposeis continuous and one to one withcompact. Thenis continuous.

Proof: Letbe any sequence inconverging toWe must show thatconverges toWritefor eachthenSince is compact, the sequenceis bounded. Letbe any convergent subsequence ofwith limitsinceis closed, and sois continuous at l, thusconverges tobutis a subsequence ofhence converges toSinceis one to one andEvery convergent subsequence ofconverges to the same limit l soconverges toand sois continuous at

We must have thatis compact, for a reason illustrated by the example below.

Let

illustrated below, is one to one and continuous on

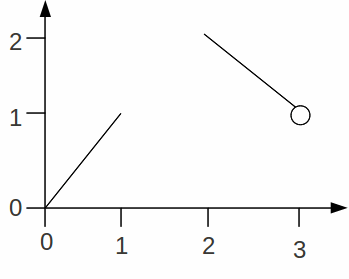
The graph ofis shown below.

Consider the sequencewhich converges to 1. For n odd,and forevensodoes not converge.