If![]() is a complex valued function on the complex plane and
is a complex valued function on the complex plane and![]() has an essential singularity at a point
has an essential singularity at a point![]() then as
then as![]() approaches
approaches![]() strange things start to happen.
strange things start to happen.![]() starts to change wildly, approaching arbitrarily close every point in the complex plane. More precisely,
starts to change wildly, approaching arbitrarily close every point in the complex plane. More precisely,
The Casorati Weierstrass Theorem
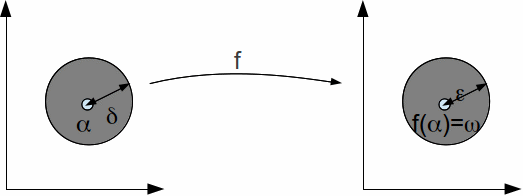
Suppose that a complex function![]() has an essential singularity at
has an essential singularity at![]() Let
Let![]() be any complex number and let
be any complex number and let![]() and
and![]() be positive real numbers. There exists
be positive real numbers. There exists![]() such that
such that![]() and
and![]()
Proof
Assume the theorem is false. Then there exists![]() and positive real numbers
and positive real numbers![]() and
and![]() such that the function
such that the function![]() is analytic on the punctured open disc
is analytic on the punctured open disc![]() and the last line does not hold, so that
and the last line does not hold, so that![]() for
for![]()
Since![]() for
for![]() the function
the function![]() is analytic. Moreover,
is analytic. Moreover,![]() for
for![]()
and so![]() has a removable singularity at
has a removable singularity at![]() so by defining
so by defining![]() appropriately, we can make
appropriately, we can make![]() analytic on
analytic on![]()
Now![]() for
for![]() and so
and so![]() for
for![]()
If![]() then
then![]() would have a removable singularity at
would have a removable singularity at![]() which could be removed by letting
which could be removed by letting![]() If
If![]() then
then![]() for some positive integer
for some positive integer![]() where
where![]() is analytic at
is analytic at![]() with
with![]() Thus
Thus
![]()
There is a stronger theorem called Picard's Theorem which states that![]() takes on all values in
takes on all values in![]() except possible one, for
except possible one, for![]()
