The Argument Principle

Letbe a function analytic on a simply connected regionand letbe a simple closed contour insuch thatforThen the winding number of about 0 is given bywhereis the number of zeros ofinsidecounted according to their orders.

Proof:

It is sufficient to prove that

(using the chain rule)

sinceis a parametrization of

this argument is only valid ifis non zero onfor then the image of each constituent smooth path ofis a constituent smooth path ofso thatis a contour. In general howevercan have zeros onbut only a finite number. By making small detours tonear the zeros ofwe can obtain a simple closed contouron whichis never zero and for which

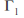1. encloses the zeros of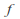as

2. 

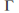
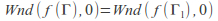
Then sincewe have

The principle can easily be extended to a contour about any point %alpha :

Letbe a function analytic on a simply connected regionand letbe a simple closed contour insuch thatforThen the winding number of aboutis given byis the number of zeros ofinsidecounted according to their order.