The Casorati Weierstrass Theorem

Ifis a complex valued function on the complex plane andhas an essential singularity at a pointthen asapproachesstrange things start to happen.starts to change wildly, approaching arbitrarily close every point in the complex plane. More precisely,

The Casorati Weierstrass Theorem

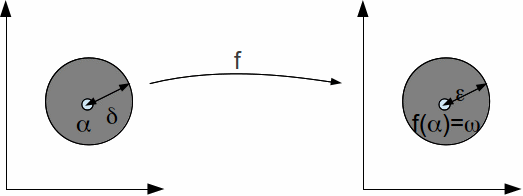
Suppose that a complex functionhas an essential singularity atLetbe any complex number and letandbe positive real numbers. There existssuch thatand

Proof

Assume the theorem is false. Then there existsand positive real numbersandsuch that the functionis analytic on the punctured open discand the last line does not hold, so thatfor

Sinceforthe functionis analytic. Moreover,for

and sohas a removable singularity atso by definingappropriately, we can make analytic on

Nowforand sofor

Ifthenwould have a removable singularity atwhich could be removed by lettingIfthenfor some positive integer whereis analytic atwithThus

There is a stronger theorem called Picard's Theorem which states thattakes on all values inexcept possible one, for