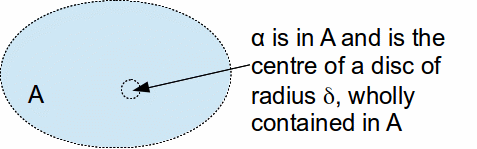
A set![]() is said to be open if every member of the set is contained in some open disc wholly contained in
is said to be open if every member of the set is contained in some open disc wholly contained in![]() More intuitively, we may say that a set is open if it does not contain its own boundary.
More intuitively, we may say that a set is open if it does not contain its own boundary.
Part of the boundary of a set may be a single point. The set![]() is open. The boundary is the circle
is open. The boundary is the circle![]() along with the single point
along with the single point![]()
If a set includes its boundary, it is said to be closed. More concisely, we may say that if![]() is a limit point of a set
is a limit point of a set![]() then
then![]() is closed if
is closed if![]() for all such
for all such![]() Obviously this is true of any point in the interior, but will be true for a closed set if
Obviously this is true of any point in the interior, but will be true for a closed set if![]() is on the boundary since any open set centred on the boundary must contain infinitely many points interior to
is on the boundary since any open set centred on the boundary must contain infinitely many points interior to![]() so is a limit point of
so is a limit point of![]() This is illustrated below.
This is illustrated below.

A set![]() is compact if it is closed and bounded. Bounded here means that there exists
is compact if it is closed and bounded. Bounded here means that there exists![]() such that
such that![]() for all
for all![]()
Example: Every set consisting of a finite set of points is compact. Every element is its own boundary, and since there are a finite number of elements, there must be a largest one,![]() so
so![]() for all
for all![]()
A set is said to be path connected if there is a path from every element of the set to every other element. A set is said to be connected if it cannot be written as the union of two open, disjoint sets. If it cannot be written as such a union, then either the two sets have a point in common, or there exists a point which is a limit point of both sets and belongs to one of the sets, so this set is not open.
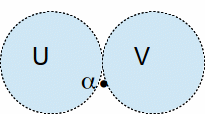
![]() and
and![]() above are disjoint except possibly for a point
above are disjoint except possibly for a point![]() If
If![]() and
and![]() then
then![]() is not connected. If
is not connected. If![]() or
or![]() or
or![]() then
then![]() is connected.
is connected.
